SOHCAHTOA

Seno, coseno y tangente

Tres funciones, la misma idea.

Triángulo rectángulo

Antes de concentrarnos en las funciones, nos ayudará dar nombres a los lados de un triángulo rectángulo, de esta manera: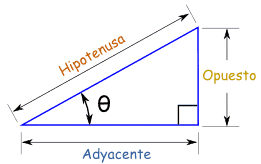

(Adyacente significa tocando el ángulo, y opuesto es opuesto al ángulo... ¡claro!)

Seno, coseno y tangente

Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente. Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son!

Para el ángulo θ :

Función seno:	sin(θ) = Opuesto / Hipotenusa
Función coseno:	cos(θ) = Adyacente / Hipotenusa
Función tangente:	tan(θ) = Opuesto / Adyacente

Nota: el seno se suele denotar sin() (por la palabra inglesa "sine") o sen(). Aquí utilizaremos sin() pero puedes encontrarte la otra notación en otros libros o sitios web.

Sohcahtoa

Sohca...¿qué? ¡Sólo es una manera de recordar qué lados se dividen! Así:

Soh...	Seno = Opuesto / Hipotenusa
...cah...	Coseno = Adyacente / Hipotenusa
...toa	Tangente = Opuesto / Adyacente

Apréndete "sohcahtoa" - ¡te puede ayudar en un examen!

Ejemplos

Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ?

El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado opuesto de longitud 1 y lado adyacente de longitud √3: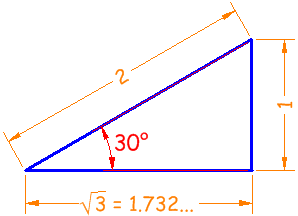

Seno	sin(30°) = 1 / 2 = 0.5
Coseno	cos(30°) = 1.732 / 2 = 0.866
Tangente	tan(30°) = 1 / 1.732 = 0.577

(¡saca la calculadora y compruébalo!)

Ejemplo 2: ¿cuáles son el seno, coseno y tangente de 45°?

El triángulo clásico de 45° tiene dos lados de 1 e hipotenusa √2: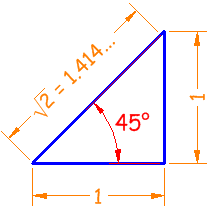

Seno	sin(45°) = 1 / 1.414 = 0.707
Coseno	cos(45°) = 1 / 1.414 = 0.707
Tangente	tan(45°) = 1 / 1 = 1

Ejercicio

Prueba este ejercicio sobre el papel donde tienes que calcular la función seno para ángulos de 0° a 360°, y dibujar el resultado. Te ayudará a entender estas funciones que son bastante simples.

Funciones menos comunes

Para completar el cuadro, hay otras 3 funciones donde divides un lado por otro, pero no se usan tanto.
Son iguales a 1 divivido entre las tres funciones básicas (sin, cos y tan), así:

Función secante:	sec(θ) = Hipotenusa / Adyacente	(=1/cos)
Función cosecante:	csc(θ) = Hipotenusa / Opuesto	(=1/sin)
Función cotangente:	cot(θ) = Adyacente / Opuesto	(=1/tan)

Videos

Videos sobre resolución de triangulos rectangulos

Triangulo Rectangulo

En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados.1 Las razones entre las longitudes de los lados de un triángulo rectángulo es un enfoque de la trigonometría plana. En particular, en un triángulo rectángulo, se cumple el llamado teorema de Pitágoras ya conocido por los babilonios.

Teorema de Pitagoras

En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

En un triángulo rectángulo, el seno y la cosecante de cualesquiera de sus ángulos agudos (x), se expresan con las razones siguientes:


Coseno y secante
En un triángulo rectangulo, las razones del coseno y la secante de cualesquiera de sus ángulos agudos (x) son:

Tangente y cotangente
La tangente y cotangente de cualesquiera de los ángulos agudos (x) de un triángulo se establece con las siguientes razones:


En el cuadro se resumen las seis funciones trigonométricas para cualquiera de los ángulos agudos de un triángulo rectángulo

Puede notarse que las funciones trigonométricas fundamentales y sus recíprocas tienen invertidos sus términos.